La paradoja de Olbers: ¿El universo es infinito? (Parte I)
- Scientia Zapata
- 19 jul 2024
- 5 Min. de lectura
Actualizado: 14 sept 2024
Los inicios la paradoja
El cielo nocturno, ese oscuro y vasto campo con estrellas que ha acompañado a la humanidad durante millones de años, es uno de los mayores misterios desde tiempos inmemorables. Seguramente, a más de uno de nosotros le han surgido preguntas como: ¿el universo es infinito? ¿el número de estrellas también lo será? O ¿por qué rayos las noches son tan oscuras si al parecer hay una infinidad de estrellas en él? Bueno, estos sin duda son cuestionamientos que por muchos siglos han llevado a dar afirmaciones y soluciones diversas, algunas con más fuerza que otras, mientras tanto, hoy intentaremos entender los inicios que dieron nacimiento a esta paradoja.

Recapitulando la historia, el matemático y astrónomo Thomas Digges fue uno de los primeros en poner el tema sobre la mesa, pensando en qué había más allá de lo propuesto por las ideas copernicanas. Así, la concepción del universo pasó al de uno “plano” y finito, al de uno profundo e infinito, pero estático (como lo veremos a lo largo de este artículo), y no sería hasta varios siglos después cuando algunas personillas lo cuestionarían. Las palabras de Digges son solo una muestra de la inevitable llegada a la paradoja:

Aquí es donde Digges, taaal vez por falta de herramientas matemáticas o sus propias limitaciones, no llega más allá. Su explicación a esto es que la mayor parte de las estrellas están muy lejos que no nos es posible verlas, con lo que sólo son visibles las que están a una distancia menor, y aunque sigue siendo una cantidad enorme, es finita. Asimismo, aunque no toma en cuenta leyes de disminución de la luminosidad con la distancia o algo parecido, su conclusión no es disparatada para la época, pero no se sostiene :(
Por fortuna, en 1610, el alemán Johannes Kepler llega a darse cuenta de ello, llegando a la idea de que sí, tal vez a mayor lejanía hubiera un brillo menor visto desde la Tierra, pero cuanto más lejos miremos, si consideramos un universo homogéneo, más estrellas hay, con lo que una cosa compensa la otra y el cielo entero debería brillar con una luminosidad deslumbrante ¿no es así? (spoiler: bueno, es claro, vemos lo contrario).
Dicho esto, la conclusión de Kepler es clara: el universo no es infinito. Existe un borde, un límite a una distancia enorme de nosotros, y ese borde es lo que vemos en negro como fondo a las estrellas fijas, que existen en un número casi infinito. Sin embargo, en uno de esos giros irónicos de la historia de la ciencia, el trabajo del propio Kepler sobre el Sistema Solar haría su explicación poco atractiva tan sólo unos años después de postularla.
... un palacio de felicidad inmóvil adornada con innumerable luces de brillo perpetuo ...
Cerca de esa época, Isaac Newton, basándose entre otras cosas en las Leyes de Kepler, llega a su Ley de la Gravitación Universal que igualmente explica el comportamiento de los cuerpos. Pero he aquí un problema: el universo aparentemente estático que observamos (sin los instrumentos de hoy día, claro, para refutarlo) no puede durar mucho con los astros sometidos a la fuerza gravitatoria, salvo que sea infinito y homogéneo. Es decir, si consideramos un borde “a la Kepler”, necesariamente hay un centro; por ende, el centro de masas del universo entero está en ese centro, e inevitablemente, todos los cuerpos del universo, incluidos la Tierra y el Sol, se verán arrastrados hacia ese centro y ¡pum! el universo colapsará sobre sí mismo.
Newton es por tanto, partidario de un universo infinito y homogéneo a gran escala, pues así no hay lugares privilegiados alrededor de los que se colapse toda su materia. Pero entonces, la única explicación a la que tal vez deberíamos llamar paradoja de Digges se va a la deriva, ¡y volvemos a las mismas!: ¿POR QUÉ el cielo nocturno es oscuro suponiendo un universo infinito y homogéneo a gran escala?
Bueno, resulta ser que, por allá de 1720, Edmund Halley propuso la primera solución a través del lente matemático, tomando en cuenta estas premisas. Mientras que en 1744, Jean-Philippe Loys de Chéseaux mejoró la idea. Esta consistía básicamente en dividir todo el Universo en una serie de cortezas esféricas tomando como centro en común a la Tierra, como las capas de una cebolla, todas del mismo grosor. De este modo, podríamos estimar la contribución al brillo del firmamento de cada una de estas “capas de cebolla”, estrella a estrella y luego capa a capa.

En resumen: una estrella situada en la “capa de cebolla” que dista r de la Tierra brilla como, con lo que cuanto más lejos esté la capa, menos brillan sus estrellas desde la Tierra. Pero para saber cuánto brilla la capa de cebolla entera, debemos multiplicar el brillo por estrella por el número de total que hay. Y por supuesto, no hay el mismo número de estrellas en cada capa.
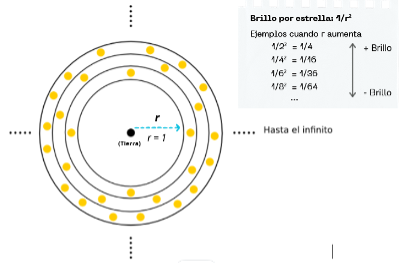
De hecho, la influencia de las regiones más lejanas de nosotros se mantiene respecto al brillo, contrario a lo que podríamos pensar. Siendo así que el brillo total es proporcional al número de estrellas multiplicado por el brillo de cada una, es decir, . Al sumar estas infinitas contribuciones de las infinitas capas el resultado es, necesariamente, un brillo infinito. ¡De vuelta al absurdo, ya que eso no se observa! Pero recobrando la calma, intentemos entender las ideas de otros personajes, alguien tarde o temprano tendría que dar con una solución cada vez más acertada ¿o no?
Así, de Chéaseaux intentó mejorar la propuesta de Halley con dos vertientes: o bien la esfera de las estrellas no era infinita o bien la intensidad de la luz disminuía rápidamente con la distancia, quizás debido a cierto material absorbente, todavía desconocido, presente en el espacio, pero solo quedó ahí.
Luego de ello, nuestro buen Heinrich Olbers, oftalmólogo retirado pero aficionado a la astronomía y quien terminaría dando nombre a esta paradoja, ofreció la siguiente explicación. Pensando en términos de rayos, si trazamos rayos rectilíneos que llegan al ojo, considerando nuevamente, un universo homogéneo e infinito, cualquiera de esos rayos acabará encontrándose con una estrella. A priori es imposible que alguno consiga escapar para siempre de ese destino final, porque al haber infinitas estrellas hasta distancias infinitas, tarde o temprano se topará con una.

Así que, en sus conclusiones, Olbers planteó la absorción de la luz de las estrellas por el polvo interestelar que encontraba en su camino hasta la Tierra, a mayor distancia que nos separa de la estrella, mayor sería la absorción. Pero digamos que esto desconcertó a John Herschel y muy probablemente hubiera pasado con Lord Kelvin: ¡En este universo se respetan las Leyes de la Termodinámica y punto!
Analizando con cuidado, de ser absorbido el brillo infinito del cielo por enormes cantidades de polvo, según el polvo absorba más y más energía se irá calentando hasta alcanzar el equilibrio térmico y brillará a su vez, emitiendo exactamente la misma cantidad de energía que absorbe y volviendo el firmamento, una vez más, infinitamente brillante. En fin, que estamos como antes… ¿o estaba la comunidad científica olvidando algo importante y ya conocido por entonces? Bueno, ese será tema para una próxima entrega del blog, así que… solo queda esperarla pronto, y, si llegaste hasta aquí, ¡Hey, gracias por leer!
Texto redactado por: Danna Paola Rivera
Público dirigido: Público de 14 años en adelante
Referencias:
Domínguez, A. et al. (2023). ¿Por qué la noche es oscura si hay infinitas estrellas? Se cumplen 200 años de la paradoja de Olbers. The Conversation. Recuperado de: https://theconversation.com/por-que-la-noche-es-oscura-si-hay-infinitas-estrellas-se-cumplen-200-anos-de-la-paradoja-de-olbers-206809#:~:text=En%20busca%20de%20explicaciones,estrella%2C%20mayor%20ser%C3%ADa%20la%20absorci%C3%B3nRevisado en junio (2024).
Gómez, P. (2011). ¿En qué consiste la paradoja de Olbers? El Tamiz. Recuperado de: https://eltamiz.com/2011/03/03/%C2%BFen-que-consiste-la-paradoja-de-olbers/ Revisado en junio (2024).
Santaolalla, J. (2018). El poeta que descifró el universo. Date un vlog. Video [YouTube]. Recuperado de: https://youtu.be/JzxHtg7jPA8?si=dpsLr55rxJSJijgd&t=1 Revisado en junio (2024).

¡Hola! soy Danna, aficionada al conocimiento y la física (aunque a veces no entienda más de lo que me gustaría), lectora, procrastinadora funcional y fiel creyente de que la ciencia y el arte están más unidos que nunca.

Comentarios